- Practice: Linear Regression
실제 Linear Regression을 수행한다
- Boston House Prices 데이터셋은 1970년대에 수 집된 보스턴 교외지역의 주택 정보를 제공
- 506개의 샘플과 다음과 같은 특성을 제공
- 1. CRIM: 도시의 인당 범죄율
- 2. ZN: 25,000평방 피트가 넘는 주택 비율
- 3. INDUS: 도시에서 소매 업종이 아닌 지역 비율
- 4. CHAS: 찰스 강 인접 여부(강 주변 = 1, 그 외 = 0)
- 5. NOX: 일산화질소 농도(10ppm당)
- 6. RM: 주택의 평균 방 개수
- 7. AGE: 1940년 이전에 지어진 자가 주택 비율
- 8. DIS: 다섯 개의 보스턴 고용 센터까지 가중치가 적용된 거 리
- 9. RAD: 방사형으로 뻗은 고속도로까지 접근성 지수
- 10. TAX: 10만 달러당 재산세율
- 11. PTRATIO: 도시의 학생-교사 비율
- 12. B: 1000(Bk - 0.63)2, 여기서 Bk는 도시의 아프리카계 미 국인 비율
- 13. LSTAT: 저소득 계층의 비율
- 14. MEDV: 자가 주택의 중간 가격(1,000달러 단위)
주택 가격(MEDV)을 추정하고자 하는 목표 변수 로 설정
from IPython.display import Image관련 라이브러리를 모두 import 시켜준다.
# pandas library를 이용해 csv 파일 읽기 (read_csv의 sep='\s+' 로 설정. 1개 이상의 whitespace 라는 뜻)
# housing dataset url : https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt',
header=None,
sep='\s+')
# 각 column은 아래와 같은 데이터를 나타냄
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()이후 판다스 라이브러리를 사용해서 데이터셋을 받아서 확인한다.

이후 데이터 사이의 관계를 살펴보기 위해서 mixtend라이브러리를 설치한다.
!pip install --upgrade mlxtend이후 데이터셋을 시각화하기 위해서 라이브러리를 import 한다
import matplotlib.pyplot as plt
from mlxtend.plotting import scatterplotmatrix이후 데이터끼리 산점도를 그려서 관계를 파악해본다.
cols = ['PTRATIO', 'LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
scatterplotmatrix(df[cols].values, figsize=(10, 8),
names=cols, alpha=0.5)
plt.tight_layout()
# plt.savefig('images/10_03.png', dpi=300)
plt.show()대강 봤을때 상관 있는것은
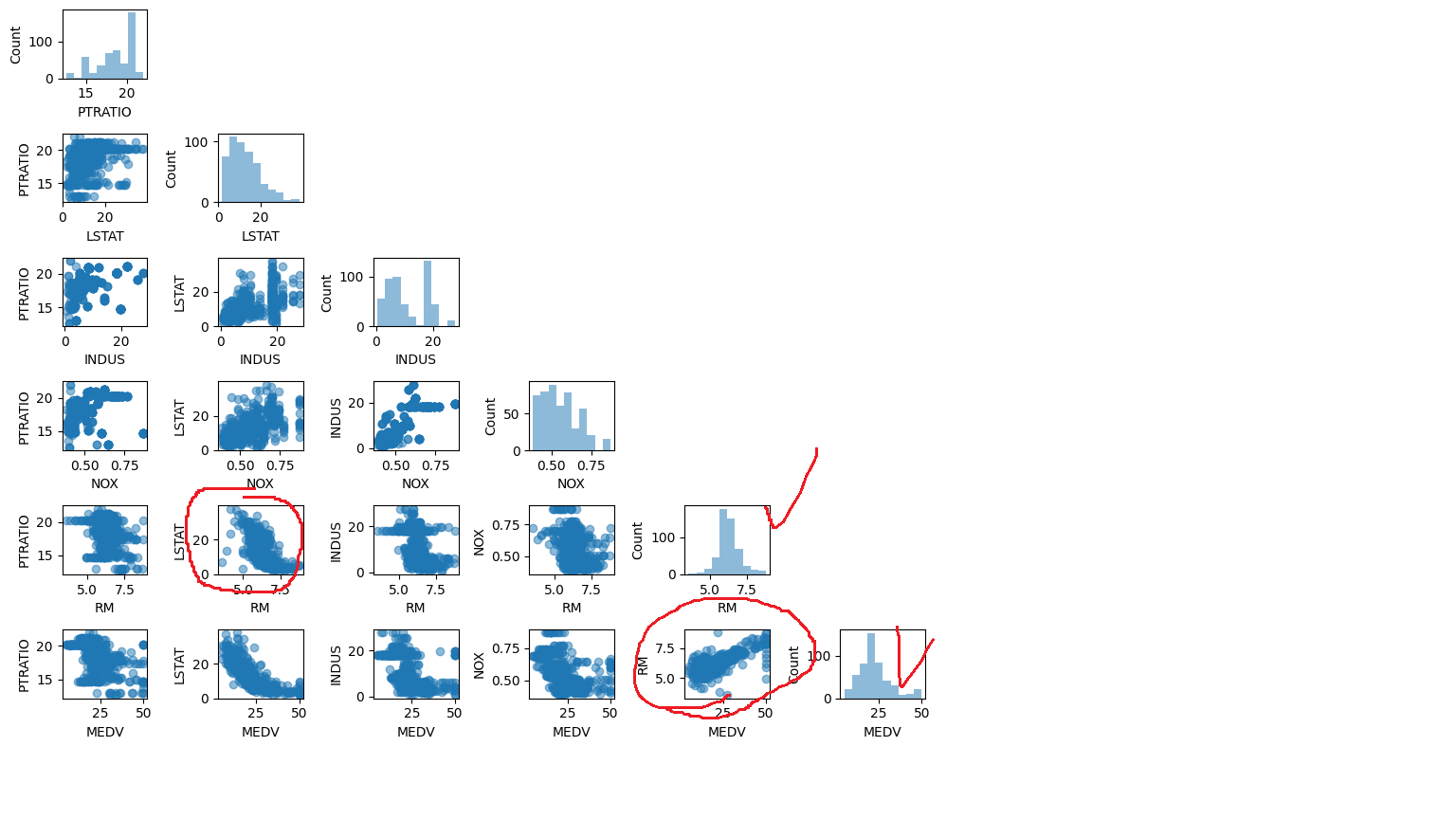
RM과 LSTAT, RM과 MEDV가 선형적인 관계를 가지고 있는 것 같고, RM,MEDV의 분포가 정규분포형으로 나와 있는 것을 관찰할수가 있다.
- Correlation Analysis: 상관분석(Correlation Analysis)이란 상관관계(Correlation)를 이용하여 두 집단 사이의 관계를 파악하는 기법. 그러니까 두 변수간에 어떤 선형적 관계를 가지는지 분석을 하는것.

상관계수(Correlation Coefficient, 𝑟)로 결정을 할수가 있는데, 상관계수는 위의 식으로 알수 있다. r은 [-1,1]의 범위를 갖는데, -1이면 음의 선형 상관관계, 1이면 양의 선형 상관관계, 0이면 그냥 상관관계가 없는거다.
이 상관계수를 행렬을 통해서 표현한다
import numpy as np
from mlxtend.plotting import heatmap
cm = np.corrcoef(df[cols].values.T)
hm = heatmap(cm, row_names=cols, column_names=cols)
# plt.savefig('images/10_04.png', dpi=300)
plt.show()를 수행하면

를 통해서 추청하고 싶은 수치인 MEDV와 상관관계가 높은(절대값이 큰) 변수는 LSTAT(-0.74)과 RM(0.70)인 것을 볼수가 있다.
이렇게 상관관계 분석을 통해서 어떤 특성을 사용해야 할지 선별이 가능하다.
이후 손실함수를 통해서
최소 제곱법 (Ordinary Least Squares): 회귀 직선으로부터 각 데이터 까지의 거리 (Residual)의 제곱합을 최소화 하는 방법
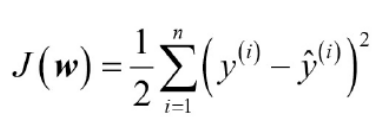
이 밖에도 다양한 최적화 기법등을 통해서 모델 파라미터를 더 세부적으로 추정을 한다.
'머신러닝' 카테고리의 다른 글
| Logistic Regression(1) (0) | 2024.04.03 |
|---|---|
| Linear Regression(1) (0) | 2024.03.25 |
| Mathematics for Machine Learning(2) (0) | 2024.03.25 |
| Mathematics for Machine Learning(1) (0) | 2024.03.23 |
| 머신러닝의 종류 (0) | 2024.03.10 |